

DOI: https://doi.org/10.46502/issn.1856-7576/2024.18.04.15
Eduweb, 2024, octubre-diciembre, v.18, n.4. ISSN: 1856-7576
Cómo citar:
Avendaño-López, P.D.U., González Torres, A., & Figueroa-Anzures, C. (2024). El impacto del aprendizaje basado en aplicaciones móviles y IA en la comprensión de variables aleatorias discretas. Revista Eduweb, 18(4), 219-240. https://doi.org/10.46502/issn.1856-7576/2024.18.04.15
The impact of mobile app-based learning and AI on understanding discrete random variables
Avendaño-López Pavel David Ulises
https://orcid.org/0000-0003-1536-1784
Tecnológico Nacional de México/ Instituto Tecnológico de Milpa Alta, Docente, Ciudad de México, México.
González Torres Arturo
https://orcid.org/0000-0002-3337-7600
Tecnológico Nacional de México/ Instituto Tecnológico de Milpa Alta, Profesor - Investigador,
Ciudad de México, México.
Autor corresponsal
Figueroa-Anzures Cynthia
https://orcid.org/0009-0009-4627-2865
cynthia.figueroa@bachilleres.edu.mx
Colegio de Bachilleres/Plantel 13 “Quirino Mendoza y Cortés”, Docente, Ciudad de México, México.
Recibido: 24/10/24
Aceptado: 19/12/24
Resumen
Este estudio analiza la enseñanza de variables aleatorias discretas utilizando la app móvil “PROBABILITY DISTRIBUTIONS” y respuestas generadas por la Inteligencia Artificial de MetaIA. Participaron 95 alumnos del CETIS 167, quienes cursan el sexto semestre en probabilidad y estadística. Se inició con la explicación de la distribución de Bernoulli para comprender eventos dicotómicos. Posteriormente, los estudiantes emplearon la app para calcular probabilidades con esta distribución y explorar conceptos relacionados con reemplazo y sin reemplazo, conectados a las distribuciones hipergeométrica y de Bernoulli, respectivamente. Además, se abordó la distribución de Poisson como proceso estocástico, empleando la app para modelar funciones de masa de probabilidad. En la etapa final, los alumnos resolvieron una evaluación de cuatro reactivos, utilizando tanto la app como MetaIA. Los resultados indicaron que los estudiantes lograron una mejor interpretación de los problemas al centrarse en el análisis conceptual más que en cálculos manuales. MetaIA mostró fortalezas en clasificar y desglosar ejercicios según distribuciones, aunque presentó errores en cálculos matemáticos debido a la falta de precisión en la integración de fuentes. Se concluye que la combinación de Tecnologías del Aprendizaje y Conocimiento con Inteligencia Artificial puede facilitar la resolución de problemas reales y promover una comprensión más profunda en los estudiantes.
Palabras clave: Variables Aleatorias Discretas, Probability Distribution, MetaIA, probabilidad, distribución Bernoulli, distribución Binomial, distribución hipergeométrica, distribución Poisson, Inteligencia Artificial.
Abstract
This study analyzes the teaching of discrete random variables using the mobile app “PROBABILITY DISTRIBUTIONS” and responses generated by MetaIA Artificial Intelligence. 95 students from CETIS 167, who are in the sixth semester of probability and statistics, participated. It began with the explanation of the Bernoulli distribution to understand dichotomous events. Later, the students used the app to calculate probabilities with this distribution and explore concepts related to replacement and without replacement, connected to the hypergeometric and Bernoulli distributions, respectively. In addition, the Poisson distribution was addressed as a stochastic process, using the app to model probability mass functions. In the final stage, the students solved a four-item evaluation, using both the app and MetaIA. The results indicated that the students achieved a better interpretation of the problems by focusing on conceptual analysis rather than manual calculations. MetaIA showed strengths in classifying and breaking down exercises according to distributions, although it presented errors in mathematical calculations due to the lack of precision in the integration of sources. It is concluded that the combination of Learning and Knowledge Technologies with Artificial Intelligence can facilitate the resolution of real problems and promote a deeper understanding in students.
Keywords: Discrete Random Variables, Probability Distribution, MetaIA, probability, Bernoulli distribution, Binomial distribution, hypergeometric distribution, Poisson distribution, Artificial Intelligence.
Introducción
En la era de la digitalización y el auge de las nuevas tecnologías, el uso de herramientas tecnológicas en la educación ha crecido exponencialmente. A nivel internacional, la inteligencia artificial (IA) se ha posicionado como un recurso fundamental en diversos campos, incluido el educativo. Países como Estados Unidos y Singapur han implementado IA en la enseñanza de matemáticas y ciencias, observando mejoras significativas en la personalización del aprendizaje y el análisis de datos. Este contexto ha fomentado la creación de diversas plataformas y aplicaciones destinadas a optimizar el proceso de enseñanza-aprendizaje en áreas complejas como la estadística y probabilidad, integrando simulaciones y cálculos automáticos que permiten una mayor comprensión de conceptos abstractos como las variables aleatorias discretas.
En México, la enseñanza de la estadística y probabilidad ha cobrado relevancia en los últimos años debido a la creciente demanda de competencias cuantitativas en distintos campos profesionales. A nivel nacional, los currículos educativos de nivel medio superior y universitario han comenzado a integrar tecnologías de aprendizaje que faciliten la adquisición de habilidades estadísticas, esenciales en disciplinas como las ciencias físico-matemáticas, ciencias sociales y administrativas, y las ciencias médico-biológicas.
El objetivo principal de este estudio es comparar la efectividad de la enseñanza de variables aleatorias discretas mediante el uso de una aplicación móvil llamada "Probability Distributions" en contraposición a las respuestas generadas por una inteligencia artificial (Meta IA). Este análisis se lleva a cabo en un grupo de estudiantes del nivel medio superior con el fin de evaluar cuál de las dos herramientas proporciona una mejor comprensión de los conceptos estadísticos y sus aplicaciones.
La justificación del estudio radica en la necesidad de utilizar tecnologías emergentes para mejorar la enseñanza de temas complejos como las distribuciones de probabilidad, donde tradicionalmente los alumnos suelen enfrentar dificultades debido a la naturaleza abstracta de los conceptos. Además, el uso de herramientas tecnológicas puede promover un aprendizaje más interactivo y significativo, mejorando la retención y comprensión del contenido.
No obstante, este estudio presenta limitantes importantes. En primer lugar, la dependencia de recursos tecnológicos como los dispositivos móviles y el acceso a internet puede afectar la implementación de las aplicaciones en zonas rurales o de bajos recursos, donde los estudiantes no siempre cuentan con las herramientas necesarias. Asimismo, la comparación entre la aplicación y la IA se limita a una evaluación cualitativa, por lo que no se abordan con profundidad los aspectos cuantitativos de cada enfoque en términos de resultados a largo plazo.
La presente investigación se articula mediante una estructura pentagonal que permite abordar de manera sistemática y rigurosa la intersección entre las tecnologías emergentes y la didáctica de la estadística. El corpus inicial desarrolla un exhaustivo marco conceptual que examina las convergencias entre los dispositivos móviles y los sistemas de inteligencia artificial en el contexto pedagógico de la estadística, con especial énfasis en las investigaciones contemporáneas sobre la enseñanza de variables aleatorias discretas. El segundo componente pormenoriza el aparato metodológico implementado, estableciendo los criterios de selección muestral, la arquitectura investigativa y el instrumental analítico empleado para la recolección y procesamiento de datos. La tercera sección presenta un análisis comparativo entre la efectividad pedagógica de las aplicaciones móviles y los sistemas de inteligencia artificial, sustentado en evidencia empírica. El cuarto segmento desarrolla una exégesis de los hallazgos obtenidos, contextualizada en el marco del acervo científico existente, estableciendo diálogos con investigaciones precedentes y delineando nuevas perspectivas interpretativas. La investigación culmina con un apartado dedicado a las inferencias derivadas del estudio, sus repercusiones en el ámbito de la praxis educativa y la formulación de directrices para futuras líneas de investigación en este campo.
Referentes teóricos o revisión de literatura
La implementación de Tecnologías o simuladores en el aula ha experimentado una amplia adopción, y de esta manera también ha generado cambios en los métodos de enseñanza y aprendizaje. Al igual que en el estudio de Álvarez Álvarez, & Jiménez Ruiz (2022), en su estudio investigo las iniciativas de educación móvil en varios países de Latinoamérica, se reconocieron 5 propuestas de Chile, 3 propuestas de Colombia, 3 propuestas de Argentina, 4 propuestas de México; y una propuesta de El Salvador, Paraguay, Honduras y Perú; todas estas se implementaron desde el 2003 hasta el 2020. Estas propuestas han facilitado la alfabetización digital de los alumnos, además de contribuir a reducir el rezago estudiantil por diferentes razones, al mismo tiempo que fomentan la motivación y la formación profesional (Álvarez Álvarez & Jiménez Ruiz, 2022).
El ChatGPT es un instrumento innovador para la enseñanza y el aprendizaje de matemáticas. En el estudio de Wardat et al. (2023), indica que llevó a cabo una investigación acerca del empleo de la herramienta, enfocándose principalmente en potenciar las capacidades matemáticas, solucionar problemas matemáticos y solucionar interrogantes de problemas geométricos. Se nota que el instrumento facilita la descomposición progresiva de los procedimientos para solucionar problemas algebraicos, integrales, derivadas y ecuaciones diferenciales. De igual manera, indica que presenta un error respecto a las cantidades mostradas, pero este inconveniente puede ser utilizado para que el estudiante desarrolle un pensamiento crítico y se aproveche a través de procedimientos. Se recomienda la utilización de preguntas concretas y una escritura sencilla, dado que pueden surgir dificultades al explorar la conversación (Wardat et al., 2023).
Mediante una revisión sobre la aplicación de la inteligencia artificial en los diversos procesos, Bolaño-García, & Duarte-Acosta (2024), determina el promedio de producción científica anual, así como los países con una mayor cantidad de publicaciones de estos. Dentro de las naciones con más publicaciones se encuentran Estados Unidos, China, Reino Unido, entre otras. Se reconocen los aspectos de ventajas y retos para la implementación de la IA, asi tambien los elementos clave de éxito, y se proponen nuevas oportunidades y posibilidades que brinda la IA en el ámbito educativo. Además, señala que es necesario ser cauteloso y estratégico, para garantizar la transparencia, la ética y la cooperación entre todos los participantes, tanto directa como indirectamente, en la educación (Bolaño-García & Duarte-Acosta, 2024).
Además, hay una variación considerable entre las versiones que se empleen de ChatGPT. Por ejemplo, en la investigación de Korkmaz Guler et al. (2024), llevó a cabo la comparación de resolución de las versiones 3.5 y 4.0 de ChatGPT, empleando un examen estandarizado de matemáticas en Turquía. Por lo general, ambas versiones recibieron respuestas instantáneas, otros ejercicios los solucionó de manera equivocada, y otros más no los solucionó ni en un primer ni en un segundo intento. No obstante, la versión 4.0 obtuvo una calificación superior. Es útil brindarle un feedback al mismo chat, para que pueda modificar y solucionar un ejercicio (Korkmaz Guler et al., 2024).
Aho-Meri (2024) llevó a cabo un estudio sobre proporcionar instrucciones de 25 temas estadísticos, de los cuales 19 se referían a conceptos estadísticos y 6 a temas avanzados de estadística. Proporcionando el mismo estímulo a inteligencias artificiales como ChatGPT y Gemini, pidió a los estudiantes que seleccionaran cual se ajusta más al concepto necesario. En el análisis de los datos, los factores que seleccionan a las Inteligencia Artificial son el valor -p, la regresión lineal, el test-t, la distribución de Cauchy, la dependencia no-linear, las derivadas y los eigenvalores. Los temas que el docente y el estudiante donde eligen de manera conjunta, a utilizar ChatGPT y Gemini son: distribución normal, coeficiente de correlación, análisis de datos funcional. Aunque los alumnos muestran una aceptación superior de las respuestas de ChatGPT para: variables aleatorias, desviación estándar, análisis de series temporales, inferencia estadística, curtosis. Los docentes suelen emplear ChatGPT para: procesos gaussianos, tendencia de series, varianza (Aho, 2024).
Pese a los múltiples beneficios que ofrece la creación de contenidos con Inteligencia Artificial como ChatGPT, también existen ciertas restricciones, tal como señala Lopezosa et al., (2024) en su estudio de España, en el que se examinaron 32 proyectos periodísticos que contaban con el respaldo de la inteligencia artificial. Es necesario establecer límites precisos en la utilización de la Inteligencia Artificial, como es escribir las demandas a cada tipo de escritura para prevenir la generación de ruido informativo. Así pues, es necesario establecer protocolos de comprobación de datos y una adecuada supervisión humana en los procesos de creación de contenido (Lopezosa et al., 2024).
En un estudio acerca de las herramientas TIC empleadas en el aula, se detecta un uso predominante en Geogebra. Según Cenich et al., (2020), selecciono a varios docentes de diferentes instituciones educativas y, mediante una entrevista, detecto la aplicación del Modelo TPACK. Este modelo fusiona tres elementos clave como son: el conocimiento del contenido de la asignatura, el saber pedagógico y el saber tecnológico. Se reconocen tres entrevistas que contemplan de manera directa la utilización de los tres componentes. Dado que posibilitan que el estudiante ejerza la manipulación libre para observar los elementos matemáticos comunes y los que varían considerablemente (Cenich et al., 2020).
En Colombia, Sarrazola (2023) señala que la utilización de chatbots como instrumentos adicionales en el aula presenta riesgos, complicaciones y ventajas. Se llevaron a cabo ejercicios de matemáticas complejas en ChatGPT 3.5, y se notó que los estudiantes pueden fomentar un razonamiento crítico, además de proporcionar una retroalimentación previa a las ideas matemáticas. Se sugiere un beneficio en el progreso del saber cuándo los docentes orienten dicho saber. Se recomienda emplear la versión ChatGPT 4 (Sarrazola, 2023).
De acuerdo con las experiencias compartidas por estudiantes y docentes originarios de México, Chile y Argentina, se llevaron a cabo prácticas en diversos temas de probabilidad y estadística, las cuales se integraron con datos de su propio entorno social y económico. El objetivo fue fomentar la intuición y el razonamiento en los procesos de manipulación de datos, tanto en estudiantes de secundaria como en los de nivel superior, así como en docentes que participaron en un curso de capacitación. Como resultado, se lograron mejoras en los rendimientos de los estudiantes, alcanzando incrementos en la efectividad de la enseñanza de los temas de probabilidad y estadística, que varian entre un 10 y 85 % (Mabel-Tauber et al., 2019).
En el estudio de Inzunza Cazares & Islas Anguiano (2019) llevado a cabo en la Universidad de Sonora, México; se sugieren cuatro actividades de estadística y el estudiante debe tener la habilidad de deducir acerca de los conceptos de población, muestreo e interpretación de estos. Por lo tanto, surge el problema con alternativas, y es posible categorizar las argumentaciones según un esquema jerárquico, los cuales se detallan a continuación. Preestructural, en la que el estudiante solo posee conceptos básicos sobre los principios estadísticos; Uniestructural, los estudiantes vinculan ciertas características de las distribuciones; multiestructural, en la que el alumno relaciona diversas características de la distribución; y relacional, en la que el alumno entiende diversas características de las distribuciones. Principalmente, se notó que los estudiantes no poseen un lenguaje estadístico formal (Inzunza Cazares & Islas Anguiano, 2019).
Estamos en un mundo complejo e incierto, en el cual día a día se incrementa la información en cualquiera de los sectores productivos. Por lo tanto, es prioridad la incorporación del estudio de la estadística y la probabilidad en los salones de clase, con el propósito de ayudar a los estudiantes en la adquisición del sentido estadístico. Es decir, unificar la cultura estadística, el pensamiento y el razonamiento estadístico (Batanero et al, 2013).
Se considera que en México la educación estadística está siendo cada vez más reconocida por su importancia en la educación de cualquier ciudadano, su inclusión en las diferentes carreras universitarias y su aportación para generar conocimiento nacional (económico, social, político, educativo y de salud) (Gómez Blancarte et al., 2022; Gal, 2007). Los siguientes elementos se consideran como las características que deben tener los estudiantes para poder aprender y aplicar la materia de probabilidad y estadística en el nivel bachillerato. Ver tabla 1.
Tabla 1.
Competencias previas del alumno.

Los currículos actuales para la educación estadística en las universidades demandan el desarrollo de habilidades de problemas mediante el uso de datos reales que permitan darle sentido al mundo que rodea a los estudiantes, lo cual requiere conocer el proceso de análisis de datos, así como promover un razonamiento y el pensamiento estadísticos. (Horton & Hardin, 2015)
La Estadística por su parte se ha convertido en las últimas décadas, en una ciencia importante, principalmente por tres razones: a) es una herramienta utilizada por muchas disciplinas, ciencias y profesiones para el desarrollo particular de sus investigaciones; b) la competitividad en el sector productivo ha generado una preocupación por darle un tratamiento estadístico a problemas de productividad y calidad en las organizaciones, aspecto que Deming (el padre del desarrollo industrial Japonés) destacó en los siguientes términos: “Ningún recurso es tan escaso como el conocimiento estadístico. No hay conocimiento que pueda contribuir tanto a mejorar la calidad, productividad y competitividad de las empresas como el de los métodos estadísticos”. (Romero Villafranca & Zunica Ramajo, 2013).
La sociedad moderna se encuentra rodeada de datos que proceden de diferentes fuentes y cuyo tratamiento implica que cada persona en su cotidianidad tenga que leer, interpretar, criticar y apropiarse de información, para lo cual se requieren algunas habilidades (alfabetización estadística). (Zapata Cardona, 2011)
Técnicas estadísticas utilizadas por ramas profesionales.
De acuerdo con el perfil profesional que el alumno de nivel bachillerato elija, se consideran los temas selectos de probabilidad y estadística a utilizar. Para las áreas de las ciencias fisicomatemáticas (FM), sociales-administrativas (SA), y médico-biológicas (MB), se consideran los temas de estadística descriptiva, inferencia estadística, regresión y correlación, análisis de series temporales, pronósticos, procesos estocásticos, análisis multivariado, análisis de supervivencia, métodos no paramétricos y resampling, métodos computacionales y simulación. Cada una de ellas tiene su propia particularidad de acuerdo con el evento aplicado. (Atlman, 1990; Rosner, 2006; Pagano & Gauvreau, 2018; Kleinbaum, & Klein, 2012; Agresti, 2018; Agresti, 2021; Moore et al., 2017; Field, 2013; Gujarati & Porter, 2009; Wooldridge, 2020; Babbie, 2021; Grimmett & Stirzaker, 2020; Ross, 2019; Durrett, 2019; Rice, 2006; Casella & Berger, 2002; DeGrooot & Schervish, 2002).
Destacando la importancia de las Variables Aleatorias Discretas (VAD), se presenta que para las ciencias físico-matemáticas, se modelan los fenómenos físicos que involucran conteos, como numero de partículas especificas en un experimento, número de piezas defectuosas en los procesos industriales. En las ciencias sociales y administrativas, las VAD son aplicadas en modelación y análisis de datos de encuestas, estudios de mercado, número de clientes para un evento favorable. Y para las ciencias médico-biológicas son de suma importancia porque permiten modelar los eventos biológicos, la detención de células específicas, infecciones en pacientes, o mutaciones presentadas en los experimentos. (Devore, 2016; Montgomery & Runger, 2018; Wasserman, 2004; Moore et al., 2017; Atlman, 1990; Agresti, 2021) En la tabla 2, se resalta los temas específicos por área.
Tabla 2.
Importancia de las VAD en las ciencias.

Cuando es necesario considerar la probabilidad del éxito y el fracaso de un solo evento, esto se define como la distribución de Bernoulli. Si aumenta el número de casos a mayor a un evento, se pueden tener dos posibilidades. Uno donde se tendrá un evento de reemplazo, donde al elegir el objeto ya no se regresa a la condición original y se calcula la distribución Hipergeométrica. Mientras que, si el objeto elegido se devuelve a la población original, se considera con reemplazo, se considera distribución binomial. Esto se muestra en la siguiente grafica.

Figura 1. Grafica de la aplicación de fenómenos dicotómicos.
(Guadarrama Bustos & Aguilar Lopez, 2021).
Por otro lado, la distribución de Poisson se utiliza para sucesos raros y aleatorios. Y dependiendo de los datos y las probabilidades de éxito, puede actuar como límite de la distribución binomial o como un proceso estocástico. Ver la figura 2.

Figura 2. Grafica de las aplicaciones de la Distribución de Poisson.
(Guadarrama Bustos & Aguilar Lopez, 2021).
El progreso de las tecnologías móviles y de inteligencia artificial (IA) ha revolucionado los modelos convencionales de enseñanza y aprendizaje, particularmente en campos que requieren de destrezas matemáticas y analíticas, como la probabilidad y la estadística. Específicamente, las variables aleatorias discretas son un asunto crucial en la evolución del pensamiento estadístico, ya que posibilitan a los alumnos entender fenómenos aleatorios y modelar situaciones prácticas de incertidumbre. Sin embargo, su instrucción frecuentemente se topa con obstáculos vinculados con la abstracción del concepto y la ausencia de recursos pedagógicos que simplifiquen su entendimiento. Las aplicaciones para dispositivos móviles y las plataformas basadas en Inteligencia Artificial, como Meta AI, proporcionan una perspectiva innovadora y enérgica para enfrentar estos retos, posibilitando un aprendizaje más interactivo y ajustado a las demandas individuales.
Aunque hay estudios anteriores que apoyan la utilización de estas tecnologías en la educación, existe una escasa comparación entre su eficacia en el aprendizaje de temas particulares, como las variables aleatorias discretas. Por una parte, las aplicaciones móviles educativas proporcionan un ambiente organizado que orienta a los alumnos mediante actividades prácticas diseñadas para potenciar sus capacidades y saberes. En contraposición, las herramientas de Inteligencia Artificial como Meta AI garantizan un aprendizaje más adaptable y personalizado, ajustándose al nivel de entendimiento y velocidad de cada usuario. En este escenario, se presenta la necesidad de determinar de manera empírica cuál de estas herramientas es más eficaz para el aprendizaje de conceptos estadísticos fundamentales en el nivel de bachillerato, especialmente en centros educativos de la Ciudad de México.
En consecuencia, este estudio propone un diseño experimental que contrasta el efecto de una aplicación móvil educativa con Meta AI en el aprendizaje de las variables aleatorias discretas. Las siguientes secciones detallan el método empleado, que abarca la elección de los participantes, los instrumentos de evaluación y los procesos de ejecución y análisis.
Metodología
Método
Se utilizó un enfoque cuantitativo, ya que el estudio se centró en la comparación de resultados numéricos obtenidos de dos herramientas: una aplicación móvil y una inteligencia artificial, para analizar el aprendizaje de variables aleatorias discretas.
Nivel de Investigación
El nivel de investigación es descriptivo y exploratorio
Es descriptivo porque el estudio se enfoca en observar, registrar y analizar cómo los estudiantes comprenden las variables aleatorias discretas a través del uso de dos herramientas: una aplicación móvil y una inteligencia artificial. Se documentan los resultados obtenidos por los alumnos y la IA, proporcionando una descripción detallada de las respuestas y su precisión, lo que permite identificar patrones de aprendizaje y comprensión.
Por otro lado, es exploratorio porque se busca indagar en un tema relativamente nuevo en el contexto educativo, que es la comparación entre tecnologías de aprendizaje (como la aplicación móvil) y la inteligencia artificial en la enseñanza de conceptos estadísticos. El estudio no se limita a describir, sino que también explora cómo estas herramientas pueden ser implementadas y qué impacto tienen en el proceso de aprendizaje, lo que abre la puerta a investigaciones futuras más profundas y cuantitativas en este campo.
Procedimiento
Selección de la muestra: Se seleccionaron 95 estudiantes del sexto semestre de la materia de probabilidad y estadística en el CETIS 167, turno vespertino.
Fases de enseñanza:
Participantes
La población estuvo constituida por 95 estudiantes del CETIS 167, de los cuales 46 eran hombres y 49 mujeres, todos cursando el sexto semestre de probabilidad y estadística.
Instrumento
Se utilizó la aplicación móvil "Probability Distributions" para enseñar a los estudiantes a manejar distribuciones estadísticas, y la inteligencia artificial MetaIA para la comparación de resultados en los ejercicios.

Figura 3. Ejemplo de figura o gráfica.
La secuencia de los temas dentro de la planificación de clases fue en el siguiente orden: Distribución aleatoria de Bernoulli, Distribución aleatoria Binomial, distribución aleatoria Hipergeométrica, y distribución aleatoria de Poisson. En cada una de las etapas se les enseño la manipulación del software, la interpretación de los resultados, la importancia de las gráficas. En cada una de las distribuciones se proporcionaron ejercicios de contextos cotidianos, y con un lenguaje sencillo y sin tecnicismos.
Para concluir se les proporciono tres ejercicios en donde el alumno debía identificar qué tipo de distribución es, y como resolverla, para finalizar debía redactar una conclusión sobre el resultado obtenido, contemplando los valores como media, varianza y lo que observaba en la gráfica. Al mismo tiempo se realiza la resolución de los mismos ejercicios utilizando la inteligencia artificial de Meta IA.
Los ejercicios por evaluar fueron los siguientes:
Se seleccionará un jurado de 12 miembros para un caso penal de un grupo de 14 hombres y 11 mujeres. ¿Cuál es la probabilidad de que el jurado esté compuesto por 6 hombres y 6 mujeres? ¿Cuál es la probabilidad de que al menos 3 jurados sean mujeres? ¿Cuál es el número esperado de mujeres? Realiza la gráfica en la aplicación Probability Distribution, determina la esperanza matemática y la varianza. REDACTA UNA CONCLUSION DE 50 PALABRAS, DE ACUERDO CON EL CONTEXTO DEL PROBLEMA
Supongamos que los nacimientos de niños y niñas tienen la misma probabilidad y que el nacimiento de cualquier niño no afecta la probabilidad del género de los demás niños. Si se seleccionan 10 nacimientos. Determinar la probabilidad de que nazcan como máximo tres niños, existan como mínimo 7 varones, existan entre 4 y 6 varones, Realiza la gráfica en la aplicación Probability Distribution. Determina la esperanza matemática y la varianza. REDACTA UNA CONCLUSION DE 50 PALABRAS, DE ACUERDO CON EL CONTEXTO DEL PROBLEMA
Se analiza el agua de un lago y se descubre que contiene, en promedio, tres bacterias por litro de agua. Se toma una muestra de 250 ml del lago. Determine la probabilidad de que la muestra de agua de 250 ml contenga exactamente dos bacterias; al menos dos bacterias; ninguna bacteria. Realiza la gráfica en la aplicación Probability Distribution, Determina la esperanza matemática y la varianza. REDACTA UNA CONCLUSION DE 50 PALABRAS, DE ACUERDO CON EL CONTEXTO DEL PROBLEMA
Se realizó una lista de cotejo para identificar los procedimientos, las gráficas y la conclusión. La guía de observación se muestra en la tabla 3.
Tabla 3.
Guía de observación para las competencias procedimentales.

La recolección de información se llevó a cabo de forma metódica, garantizando consistencia en la valoración de ambos grupos y minimizando posibles prejuicios durante el proceso de observación. Con estos instrumentos metodológicos, se intentó adquirir datos exactos y comparativos acerca de la eficacia de cada método tecnológico en el proceso de aprendizaje de los alumnos.
Resultados y discusión
Para el primer ejercicio se tiene como contexto un jurado el cual debe estar constituido por 12 personas, se tiene una población inicial de 25 personas, de las cuales son 14 hombres y 11 mujeres. Se identifica que es un muestreo sin reemplazo, además de que los elementos de éxito y de fracaso pueden hombres y mujeres en el mismo conjunto respuesta. Por lo tanto, se trata de una distribución hipergeométrica. Luego, la función de masa de probabilidad es la ecuación siguiente

De acuerdo con esto la probabilidad de que el jurado este compuesto por 6 mujeres y 6 hombres, es la siguiente:

Lo cual se corrobora con la aplicación. Ver figura 4.
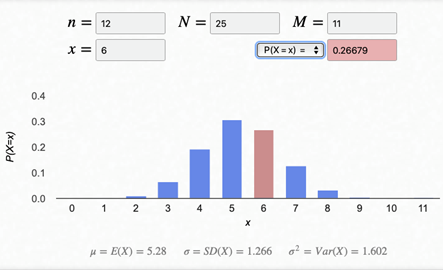
Figura 4. Grafica de la distribución hipergeométrica, para P(X=6).
Para el cuestionamiento sobre la probabilidad de que al menos 3 mujeres sean elegidas, modifica la ecuación de la siguiente manera

A continuación, se muestra la gráfica obtenida, figura 5.

Figura 5. Grafica de la distribución hipergeométrica, para P(X>=3).
Para el ultimo cuestionamiento sobre el numero esperado de mujeres, solo basta observar la parte baja de la imagen anterior y menciona que es E(X)=5.28.
Comparando la respuesta con los alumnos, los datos obtenidos son los siguientes: En el primer caso se identifica la probabilidad de que seis mujeres participen como parte del jurado. En el segundo inciso se presentan complicaciones al manejar el juego de palabras como “de que al menos” o “a lo mucho”. Por lo tanto, se observa que solo determina la probabilidad para que tres mujeres exactamente participen como parte del jurado. Otro de los puntos donde se presenta confusión es con la esperanza matemática. Ya que el dato si lo redacto, pero no pudo interpretarlo. Para la redacción de una conclusión general, el estudiante logra identificar que este tipo de fenómenos sociales, involucran una probabilidad que relativamente es mínima. Ver figura 6.

Figura 6. Repuesta de un alumno para la distribución hipergeométrica.

Figura 7. Repuesta de Meta IA para la distribución hipergeométrica.
Este mismo ejercicio se redactó en Meta IA, obteniéndose un análisis previo para determinar el tipo de Distribución a utilizar, para este caso es la hipergeométrica. Logra identificar la población, el tamaño de muestra, y la variable prueba, que fueron las mujeres. Se propone el método de resolución, de los incisos a, y b, sin embargo, presentan una diferencia del 11 % con respecto al valor real. El inciso c lo determinan correctamente. La IA no puede generar una gráfica de las probabilidades, y también se observa en el conjunto de probabilidades un error. Donde el valor real es de P(X=3) =0.06352, mientras que la IA obtiene un valor de P(X=3) =0.206.
IA redacta una conclusión combinando todos los elementos calculados. A lo cual, al estudiante, le cuesta trabajo el poder redactar 50 palabras. Ver figuras 7 y 8.

Figura 8. Repuesta de Meta IA para la distribución hipergeométrica.
El segundo ejercicio, tiene como contexto el nacimiento de una persona, que puede ser del género femenino o masculino. Se determina que la presentarse solo dos posibles eventos, y 10 experimentaciones, será una distribución binomial. A la vez, menciona que la probabilidad de que sea varón o mujer es la misma, por lo tanto, p y q serán iguales a 0.5. por lo tanto, la función de probabilidad de masa será la siguiente:

Para determinar la probabilidad de que como máximo nazcan tres niños, se determina de la siguiente manera.

La grafica se muestra en la figura 9.
Para el inciso b, el resultado es similar, ya que al tener la misma probabilidad de éxito y de fracaso se comporta como una curva simétrica. Entonces la probabilidad de que nazcan como mínimo 3 varones de 0.17188. Para la probabilidad de que nazcan entre 4 y 6 varones se realiza con la sumatoria por lo tanto es 0.65625. La esperanza matemática se observa en la figura anterior la cual es de E(X)=5 niños y la varianza es de 2.5. El alumno en su resolución logra calcular las probabilidades de que como máximo nazcan tres niños y como mínimo 7 varones. Al propone un rango, solo determino un solo valor. Ver figura 10.

Figura 9. Grafica de la distribución binomial sobre el nacimiento.

Figura 10. Repuesta de un alumno para la distribución binomial.
Se puede observar que META IA, no puede generar de manera inmediata, los cálculos a pesar de determinar la distribución binomial. Pero presenta los pasos para poder generar la gráfica en la aplicación Probability Distribution. Ver figuras 11 y 12.
Para la distribución se Poisson se observa los siguiente. Menciona que existe 3 bacterias por cada litro de agua de un lago. Y se obtiene una muestra de 250 ml, por lo tanto, se tiene que existen 3 bacterias por cada 1000 ml.
Se tiene un suceso raro, y por lo tanto, es una distribución de Poisson, la cual actúa como procesos estocástico ya que se trata de muestreo por volumen. Se tiene que identificar el promedio de bacterias que pudieran existir por cada 250 ml, la cual viene de referencia del muestreo.

Figura 11. Repuesta de Meta IA para la distribución binomial.

Figura 12. Repuesta de Meta IA para la distribución binomial.
Se tiene

Por lo tanto, la función de probabilidad de masa esta generada por:

La grafica de la función es la figura 13.
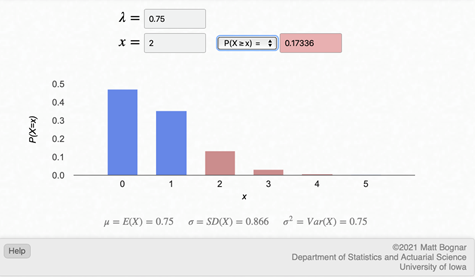
Figura 13. Grafica de la distribución de Poisson de bacteria en el agua.
Para la identificación de dos bacterias exactamente en la muestra de agua, se tiene el siguiente calculo,

Para determinar que al menos dos bacterias se encuentran en la muestra, se calcula la probabilidad de que existan menos de 2 bacterias.

La probabilidad es de 0.1733: por otro lado, la probabilidad de que no se encuentre ninguna bacteria en la muestra es de

Por parte de los alumnos, se observó una resolución incorrecta. Donde no tuvieron la capacidad de identificar la distribución de Poisson, y se consideró o binomial o hipergeométrica. Figura 14.

Figura 14. Repuesta de un alumno para la distribución Poisson.
Por parte de Mate IA, se observa que identifica correctamente la distribución por la cual se debe calcular. Identifica de manera correcta el promedio de bacterias por los 250 ml de muestreo. a pesar de redactar de manera correcta la ecuación de resolución, al determinar el valor obtuvo un error del 38 %, para la primera respuesta. Muy diferente a la obtenida con la distribución hipergeométrica. En la segunda respuesta se presenta un error del 17%. Para la probabilidad de no encontrar bacterias, se obtiene el resultado correcto, pero también se observa que es una ecuación matemática sencilla. Ver figura 15 y 16.

Figura 15. Repuesta de Meta IA para la distribución binomial.

Figura 16. Repuesta de Meta IA para la distribución binomial.
Como característica positiva se observa, que el alumno puede recibir una asistencia en tiempo real para poder desglosar o determinar las características principales para identificar los elementos de cada una de las distribuciones aleatorias discretas.
De acuerdo con los resultados obtenidos se califica de la siguiente manera la guía de observación, tabla 4.
Tabla 4.
Datos comparativos.

Se pueden plantear problemas complejos al ChatGPT y trabajar en equipo para descomponer el problema en pasos más manejables; además, la IA les puede ayudar a los estudiantes a identificar errores comunes y proporcionar sugerencias para corregirlos (Gavira Durón, 2023).
Pero se deberá tener cuidado con los riesgos ante los que estamos expuestos tanto los estudiantes como los profesores por el mal uso y abuso que se realiza con dicha herramienta que, sin una guía adecuada, puede generar soluciones erróneas en problemas matemáticos de alto nivel, además de que se puede perder el pensamiento crítico (Sarrazola, 2023).
Gracias a la mediación de la tecnología en los procesos de enseñanza y aprendizaje, es el docente quien se convierte en el epicentro de este proceso puesto que es éste quien autorregula el transcurso de la acción. Es decir, que gracias a las inmensas posibilidades que ofrece la tecnología se puede adaptar y personalizar la mediación educativa, lo cual repercute en el desarrollo de su aprendizaje (Martinez-Baquero & Rodríguez-Umaña, 2022).
Desde esta perspectiva se requiere la necesidad de posicionar el celular como un recurso más del proceso pedagógico, se debe concientizar al estudiante en el uso racional y responsable considerándolo como una estrategia para vencer la apatía hacia el aprendizaje y mostrarles que las nuevas tecnologías no sólo sirven para entretenerse, sino que también pueden ser un aliado en la construcción del conocimiento. (Dillan, 2011; Álvarez Álvarez & Jiménez Ruiz, 2022)
Por lo tanto, será necesario en trabajos posteriores de importancia proponer una planeación didáctica que involucre a las aplicaciones móviles trabajando en conjunto con la inteligencia artificial de Meta IA. Con la finalidad de apoyar el aprendizaje y aplicaciones de los conceptos matemáticos dentro del salón de clases.
Los hallazgos mostraron variaciones notables en el rendimiento entre la aplicación móvil y la Meta IA. Aunque la aplicación móvil sobresalió en el fortalecimiento de destrezas prácticas y la solución de ejercicios estructurados, Meta AI demostró una mayor eficacia en promover el pensamiento crítico y la capacidad de adaptación en diversos contextos. Estos descubrimientos evidencian la simbiosis de ambas herramientas y enfatizan la relevancia de elegir recursos tecnológicos que concuerden con los objetivos concretos de aprendizaje. En la siguiente sección se examinan en profundidad estas implicaciones, teniendo en cuenta las fortalezas y restricciones de cada método, y se muestran las conclusiones globales del estudio, junto con sugerencias para futuros estudios y usos educativos.
Conclusiones
De acuerdo con el análisis y discusión de resultados obtenidos, de la comparación de la efectividad de las actividades de enseñanza aprendizaje con las Tecnologías del Aprendizaje y el Conocimiento, y la aplicación MetaIA, se obtuvieron las siguientes conclusiones. Al proponer el uso de la aplicación estadística, se ahorra tiempo en estar manipulando copias para cada una de las tablas y se puede enfocar al alumno en los procedimientos, análisis y en la contextualización del problema.
Se observó que los estudiantes lograron interpretar mejor los resultados al utilizar la aplicación móvil “Probability Distributions”, enfocándose más en el análisis y la comprensión conceptual que en los cálculos matemáticos mecánicos. Esto coincide con estudios previos que destacan cómo las tecnologías de aprendizaje pueden facilitar la adquisición de habilidades estadísticas y matemáticas complejas al permitir una interacción más dinámica y visual con los datos (Álvarez Álvarez & Jiménez Ruiz, 2022; Horton & Hardin, 2015). Sin embargo, también se detectaron áreas de mejora, como la dificultad para identificar correctamente las distribuciones en contextos menos comunes (e.g., Poisson), lo cual sugiere la necesidad de una instrucción guiada más sólida.
Por otro lado, la IA MetaIA mostró un desempeño mixto. Aunque identificó correctamente las distribuciones en la mayoría de los casos y desglosó los cálculos paso a paso, presentó errores en los procedimientos matemáticos y resultados numéricos (por ejemplo, una diferencia del 11 % en la distribución hipergeométrica). Esto se alinea con investigaciones previas que advierten sobre la falta de precisión de las IA en problemas específicos y su dependencia de bases de datos no siempre confiables (Wardat et al., 2023; Sarrazola, 2023). No obstante, su capacidad para clasificar ejercicios y ofrecer retroalimentación estructurada representa un apoyo potencial para complementar el aprendizaje autónomo de los estudiantes.
A partir de estos hallazgos, se concluye que una integración efectiva de tecnologías de aprendizaje e IA en el aula requiere de una planeación didáctica que contemple sus limitaciones y fortalezas. Es fundamental que los docentes actúen como mediadores en el uso de estas herramientas, promoviendo su uso crítico y ético, y guiando a los estudiantes en el proceso de toma de decisiones y resolución de problemas (Martinez-Baquero, 2022). Asimismo, sería útil incorporar actividades colaborativas en las que los estudiantes trabajen en equipo con el apoyo de IA, lo que podría potenciar tanto su comprensión como su razonamiento crítico (Gavira Durón, 2023).
Finalmente, es importante señalar que esta investigación abre la puerta a estudios más amplios y profundos que evalúen el impacto cuantitativo y cualitativo de estas herramientas en la enseñanza de estadística. Futuras investigaciones podrían explorar el impacto a largo plazo de estas metodologías en el desarrollo de habilidades estadísticas o su aplicación en otras disciplinas.
Referencias bibliográficas
Agresti, A. (2018). An Introduction to Categorical Data Analysis. Wiley.
Agresti, A. (2021). Statistical Methods for the Social Science. Pearson Education.
Aho, M. (2024). On the quality of mathematical writing produced by ChatGPT and Gemini (Tesis Masters programme in engineering Physics an Matehamtics) Aalto University. Repositorio Institutcional de la Aalto University. https://aaltodoc.aalto.fi/server/api/core/bitstreams/663f70f0-4206-49b0-bdf3-1893109b4a65/content
Álvarez Álvarez, E., & Jiménez Ruiz, L. K. (2022). Aprendizaje móvil mediado por apps: Impacto para la innovación en ambientes educativos en América Latina. Revista de Investigación en Ciencias de la Educación, Horizontes, 6(26), 1-14. https://doi.org/10.33996/revistahorizontes.v6i26.490
Atlman, D. G. (1990). Practical Statistics for Medical Research. Chapman & Hall/CRC.
Babbie E. R. (2021). The Practice of Social Research. Cengage Learning.
Batanero, C., Diaz, C., Contreras, J. M., & Roa, R. (2013). El sentido estadístico y su desarrollo. Números: Revista de Didáctica de las Matemáticas, (83), 7-18. https://drive.google.com/file/d/1wBh0ttAwK02g3AS66terPWi48hxlEKqL/view
Bolaño-García, M., & Duarte-Acosta, N. (2024). Una revisión sistemática del uso de la inteligencia artificial en la educación. Revista Colombiana de Cirugía, 39(1), 51-63. https://doi.org/10.30944/20117582.2365
Casella, G., & Berger, R.L. (2002). Statistical Inference (2nd Edition). Thomson Learning Inc.
Cenich, G., Araujo, S., & Santos, G. (2020). Conocimiento tecnológico pedagógico del contenido en la enseñanza de matemática en el ciclo superior de la escuela secundaria. Perfiles educativos, 42(167), 53-67. https://doi.org/10.22201/iisue.24486167e.2019.167.59276
DeGrooot, M. H., & Schervish, M. J. (2002). Probability and Statistics. Addison-Wesley.
Devore, J. L. (2016). Probability and Statistics for Engineering and the Sciences. Cengage Learning.
Dillan, A. (2011). Celulares ¿Aliados o enemigos? Revista Clarin-educación, 18(2), 1-4. https://pdfcoffee.com/celulares-aliados-o-enemigos-clarin-2-pdf-free.html
Durrett, R. (2019). Probability Theory and Examples. Cambridge University Press.
Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics: And Sex and Drugs and Rock “N” Roll (4th Edition). Sage.
Gal, I. (2007). Adults' Statistical Literacy: Meanings, Components, Responsibilities. International Statistical Review, 70(1). 1-25. https://doi.org/10.1111/j.1751-5823.2002.tb00336.x
Gavira Durón, N. (2023). Cómo potenciar las habilidades matemáticas con ChatGPT. Revista Mexicana De Bachillerato a Distancia, 15(30), 1-5. https://doi.org/10.22201/cuaieed.20074751e.2023.30.86525
Gómez Blancarte, A. L., Chávez Aguilar, R. D., & Miranda Viramontes, I. (2022). Enfoques de la enseñanza de la estadística en los programas de estudio de educación media superior. IE Revista De Investigación Educativa De La REDIECH, 13, 1-24. https://doi.org/10.33010/ie_rie_rediech.v13i0.1394
Grimmett, G., & Stirzaker, D. (2020). Probability and Random Processes. Oxford University Press.
Guadarrama Bustos, L., & Aguilar Lopez, M. A. (2021). Introduccion al Analisis Estadistico. Centro de Investigacion en Matematicas.
Gujarati, D.N., & Porter, D.C. (2009). Basic Econometrics (5th Edition). McGraw Hill.
Horton, N. J., & Hardin, J. S. (2015). Teaching the Next Generation of Statistics Students to “Think With Data”: Special Issue on Statistics and the Undergraduate Curriculum. The American Statistician, 69(4), 259–265. https://doi.org/10.1080/00031305.2015.1094283
Inzunza Cazares, S., & Islas Anguiano, E. (2019). Análisis de una trayectoria de aprendizaje para desarrollar razonamiento sobre muestras, variabilidad y distribuciones muestrales. Educación matemática, 31(3), 203-230. https://doi.org/10.24844/EM3103.08
Kleinbaum, D. G. & Klein, M. (2012). Survival Analysis. A self-Learning Text. Statistics for Biology and Health. Springer. http://www.uop.edu.pk/ocontents/survival-analysis-self-learning-book.pdf
Korkmaz Guler, N., Dertli, Z. G., Boran, E., & Yildiz, B. (2024). An artificial intelligence application in mathematics education: Evaluating ChatGPT’s academic achievement in a mathematics exam. Pedagogical Research, 9(2), 1-12. https://doi.org/10.29333/pr/14145
Lopezosa, C., Pérez-Montoro, M., & Rey Martín, C. (2024). El uso de la inteligencia artificial en las redacciones: propuestas y limitaciones. Revista De Comunicación, 23(1), 279–293. https://doi.org/10.26441/RC23.1-2024-3309
Mabel-Tauber, L., Alvarado Martínez, H., Zapata-Cardona, L., Pinto Sosa, J. E., & Albert Huerta, A. (2019). Experiencias de enseñanza sobre probabildiad y estadistica. Propuestas paa la enseñanza de mateamticas. Acta Latinoamericana de Matematica Educativa, 32(1), 316-326. https://funes.uniandes.edu.co/wp-content/uploads/tainacan-items/32454/1153463/Mabel2019Experiencias.pdf
Martinez-Baquero, J. E., & Rodríguez-Umaña, L. A. (2022). Uso de aplicaciones móviles como herramienta de apoyo tecnológico para la enseñanza con metodología steam. Revista Politécnica, 18(36), 75–90. https://doi.org/10.33571/rpolitec.v18n36a6
Montgomery, D. C., & Runger, G. C. (2018). Applied Statistics and Probability for Engineers. John Wiley & Son.
Moore, D. S., McCabe, G. P., y Alwan, L. (2017). Introduction to the Practice of Statistics (9th Edition). W.H. Freeman and Company.
Pagano, M., & Gauvreau, K. (2018). Principles of Biostatistics (2nd ed.). Chapman and Hall/CRC. https://doi.org/10.1201/9780429489624
Rice, J. A. (2006). Mathematical Statistics and Data Analysis. Thomson/Brooks/Cole.
Romero Villafranca, R., & Zunica Ramajo, L. (2013). Metodos estadisticos para ingenieros. Editorial Universitat Politècnica de València.
Rosner, B. (2006). Fundamentals of Biostatistics. Cengage Learning.
Ross, S. M. (2019). Introduction to Probability Models. Academic Press.
Sarrazola, A. (2023). Uso de ChatGPT como herramienta en las aulas de clase. Revista EIA, 20(40), 1–23. https://doi.org/10.24050/reia.v20i40.1708
Sulym, V., Melnykov, A., Popov, M., Vechirko, O., & Malets, D. (2023). Improving education through implementation of information technologies into the educational process. Amazonia Investiga, 12(68), 281–293. https://doi.org/10.34069/AI/2023.68.08.26
Wardat, Y., Tashtoush, M. A., AlAli, R., & Jarrah, A. M. (2023). ChatGPT: A revolutionary tool for teaching and learning mathematics. Eurasia Journal of Mathematics, Science and Technology Education, 19(7), 1-18. https://doi.org/10.29333/ejmste/13272
Wasserman, L. (2004) All of Statistics. A Concise Course in Statistical Inference. Springer.
Wooldridge, J. M. (2020). Introductory Econometrics: A Modern Approach. Cengage Learning.
Zapata Cardona, L. (2011). ¿Cómo contribuir a la alfabetización estadística? Revista Virtual Universidad Católica Del Norte, 1(33), 234–247. https://revistavirtual.ucn.edu.co/index.php/RevistaUCN/article/view/4

Este artículo está bajo la licencia Creative Commons Atribución 4.0 Internacional (CC BY 4.0). Se permite la reproducción, distribución y comunicación pública de la obra, así como la creación de obras derivadas, siempre que se cite la fuente original.